人的DNA不仅仅是指导生长和发育的蓝图,更是一本详细记录了人类祖先集体旅程的日志。它包含了关于古代种群是繁荣兴盛、艰难求生还是迁徙流动的微妙线索。这引出了一个核心问题:我们能否仅仅通过分析一个现代人的DNA,就估算出数千年甚至数百万年前我们祖先种群的规模大小?
自本世纪以来,生物信息学蓬勃发展,科学家创造性地发明了众多解读基因组历史的工具。其中,**成对序列马尔可夫溯祖模型(Pairwise Sequentially Markovian Coalescent, PSMC)算法无疑是一项里程碑式的成就。由李恒(Heng Li)和理查德·德宾(Richard Durbin)于2011年提出,PSMC的神奇之处在于,它仅需一个个体的二倍体基因组序列,就能重建其所属种群在过去漫长时间里的有效种群大小(effective population size, (N_e))**的动态变化历史。这种"以少见多"的能力,与许多需要大量个体样本的方法形成了鲜明对比。
自诞生以来,PSMC已被广泛应用于研究人类、古人类(如尼安德特人和丹尼索瓦人)、各种动物(如古代马、狼、猛犸象、鸟类、熊、猿类、熊猫等) 甚至植物的种群历史,尤其擅长揭示远古时期的种群动态。它还能帮助推断物种分化时间、估算突变率等关键进化参数。
本文将带您深入了解PSMC算法。我们将首先介绍其背后的核心生物学概念——溯祖理论和基因重组——然后解释PSMC如何巧妙地运用**隐马尔可夫模型(HMMs)**从基因组序列中提取历史信息,展示它揭示了哪些有趣的发现,探讨它的局限性,并展望该领域的后续发展。
基因组:一部由重组和溯祖书写的历史文献
想象一下我们的基因组。对于大多数染色体(除了性染色体),我们从父母双方各继承一套。然而,由于在世代传递过程中发生的基因重组(recombination)导致我们从父母那里继承的染色体并非完整的"父本版"或"母本版",而是由来自更早祖先的不同片段拼接而成的"镶嵌片段"。这意味着,沿着同一条染色体,不同的片段可能拥有截然不同的祖先和历史故事。
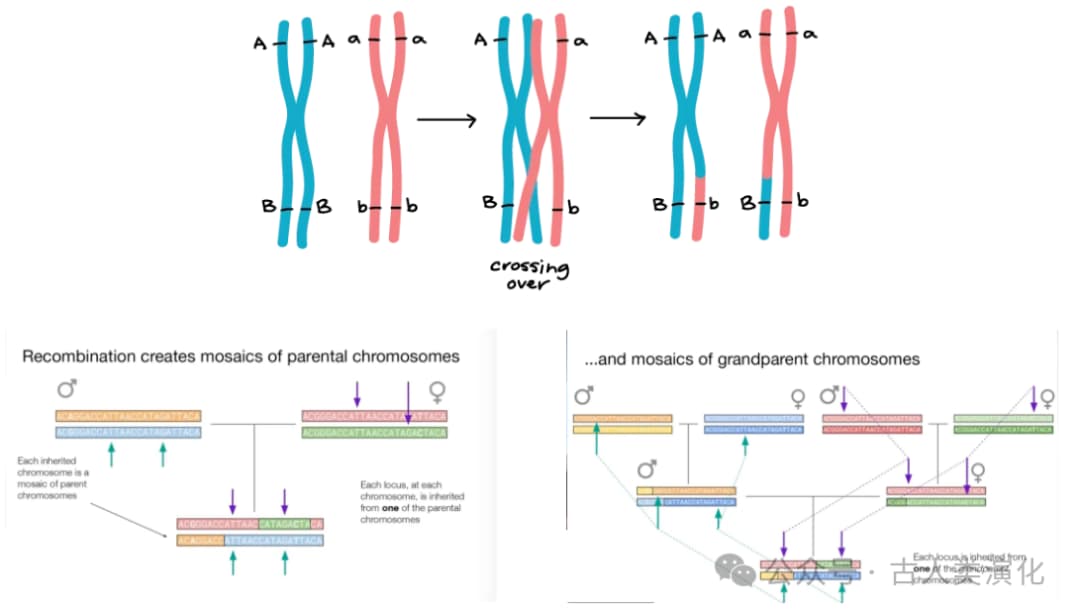
为了理解这些片段的历史,我们需要引入溯祖理论(Coalescent Theory)。与传统的从祖先看向后代的视角不同,溯祖理论采取"回溯时光"的方式。它追踪样本中等位基因(基因的不同版本)的谱系(lineages),看它们如何在过去的世代中逐渐合并(coalesce),最终汇聚到一个共同的祖先。对于任意一对谱系,它们最终相遇的那个共同祖先的时间点,被称为最近共同祖先时间(Time to Most Recent Common Ancestor, TMRCA)。
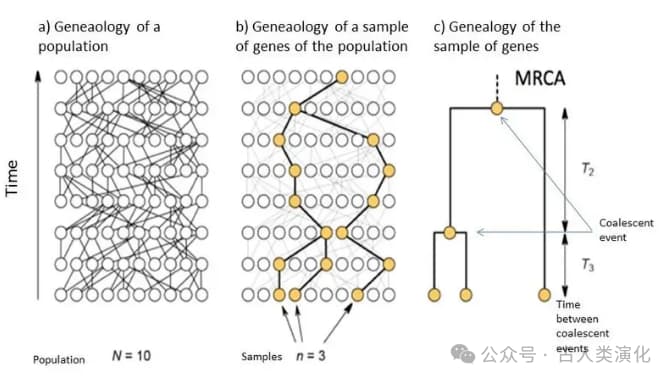
溯祖理论的核心在于它揭示了谱系合并速率与**有效种群大小((N_e))**之间的深刻联系 。有效种群大小可以理解为一个理想化的、随机交配的群体规模,该群体经历的遗传漂变程度与实际种群相同。简单来说:
- 在一个小的有效种群中,个体间的亲缘关系更近,任意两个基因谱系更容易在较近的过去找到共同祖先。因此,谱系合并(coalescence)发生得更快,平均TMRCA更短。
- 在一个大的有效种群中,个体间的亲缘关系相对疏远,谱系需要追溯更长的时间才能找到共同祖先。因此,谱系合并发生得更慢,平均TMRCA更长。
这个反比关系是利用基因组信息推断种群历史的基础。理论上,两个谱系发生合并的概率与(1/(2N_e))成正比。
但是,溯祖理论告诉我们,合并速率与种群大小有关,这意味着我们需要观察多个谱系的合并事件才能推断历史。而PSMC仅使用一个个体的基因组(也就是两套同源染色体)。那么,它是如何获得足够的信息来推断整个种群的历史呢?答案就在于基因重组的力量。正是因为基因重组将个体的两条染色体切割并重组成无数个具有不同祖先历史的片段 ,导致了沿着基因组的不同位置,这两条染色体对应片段间的TMRCA是不同的,这些不同的TMRCA值反映了它们各自发生合并时(即不同历史时间点)的有效种群大小 。因此,通过分析单个个体基因组上TMRCA的分布和变化,PSMC实际上采样了大量来自过去的、独立的成对溯祖事件信息。基因重组巧妙地将一个二倍体基因组转化为了研究种群历史的丰富数据源,这就是PSMC能从"一"窥"全"的关键所在。
揭开隐藏的历史:隐马尔可夫模型(HMM)的魔力
要从基因组序列(我们能看到的)推断出隐藏在其中的TMRCA历史(我们看不到的),PSMC借助了一种强大的统计工具——隐马尔可夫模型(Hidden Markov Model, HMM)。
我们可以用一个简单的例子来理解HMM 。假设你想知道某天的天气(晴天还是雨天),但你被关在一个没有窗户的房间里,唯一能观察到的是外面的人当天吃了多少冰淇淋。在这个例子中:
- 隐藏状态(Hidden States): 你无法直接观测到的真实情况,即天气(晴天/雨天)。
- 观测值(Observations / Emissions): 你能看到的数据,由隐藏状态产生,即冰淇淋的销量(比如1个、2个、3个)。
- 转移概率(Transition Probabilities): 隐藏状态之间转换的可能性。例如,今天晴天,明天仍然晴天的概率是多少?今天晴天,明天转为雨天的概率又是多少?
- 发射概率(Emission Probabilities): 在某个隐藏状态下,产生特定观测值的可能性。例如,如果是晴天,人们吃3个冰淇淋的概率是多少?如果是雨天,吃1个冰淇淋的概率又是多少?
HMM的核心思想是,通过分析观测值的序列(连续几天的冰淇淋销量),结合我们对转移概率(天气变化的规律)和发射概率(天气如何影响吃冰淇淋行为)的了解(或估计),来推断最有可能的隐藏状态序列(那几天的真实天气)。
HMM还包含一个重要的马尔可夫假设(Markov Property):当前状态只依赖于前一个状态,而与更早的状态无关。就像预测明天的天气只需要知道今天的天气一样。在基因组分析中,这意味着一个位置的TMRCA主要受其紧邻前一个位置的TMRCA和两者之间是否发生重组的影响。虽然这对基因组来说是一个近似(被称为SMC近似),但实践证明它非常有效。
PSMC如何工作:基因组上的HMM
现在我们将HMM的概念具体映射到PSMC算法上:
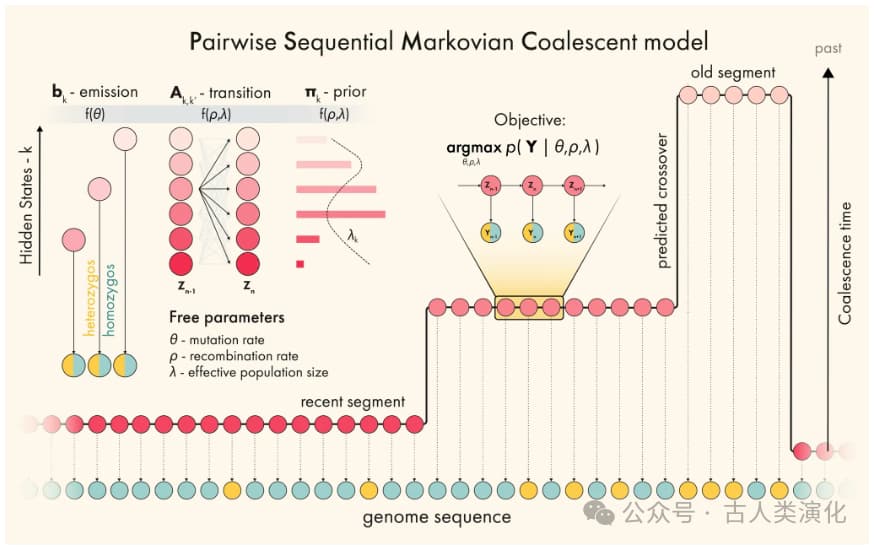
- 隐藏状态: 离散化的TMRCA。由于TMRCA是连续的时间值,而标准HMM要求状态是离散的,PSMC将时间回溯划分为多个(例如32或64个)不重叠的时间区间 。每个区间代表一个隐藏状态,表示基因组某个位置的两条链的共同祖先落在这个时间段内。
- 观测值 (发射): 局部杂合度(heterozygosity)。PSMC将基因组划分为许多小的窗口(例如100bp)。在每个窗口内,算法检查这个二倍体个体的两条染色体在该窗口是否存在差异(即杂合位点)。如果存在至少一个差异,该窗口就被标记为"杂合"(例如用'K'或'1'表示);如果没有差异,则标记为"纯合"(例如用'T'或'0'表示)。这样,整个基因组就被转换成一串由0和1(或T和K)组成的观测序列,作为HMM的输入。
- 发射概率: 给定TMRCA状态,观测到杂合的概率。这个概率主要取决于两个因素:隐藏的TMRCA状态和突变率((\mu))。TMRCA越长,意味着两条谱系分开的时间越久,积累突变的机会就越多,因此在该窗口观察到杂合位点的概率就越高。PSMC模型中,这个概率通常与(2\mu t)相关(其中t是TMRCA)。更准确地说,它与群体突变率(\theta = 4N_e\mu)有关。
- 转移概率: 从一个TMRCA状态转移到另一个状态的概率。这主要由重组率((\rho))决定。当算法沿着染色体从一个窗口移动到下一个窗口时,如果在这两个窗口之间发生了祖先重组事件,那么下一个窗口的TMRCA就可能与前一个窗口不同,从而导致隐藏状态的转移。转移的概率不仅取决于重组率,还与发生重组时的种群历史(影响重组后新谱系的合并概率)有关。
PSMC的工作流程可以概括为:
- 输入: 将个体的二倍体基因组序列处理成表示杂合/纯合状态的序列(例如,每100bp一个标记)。
- HMM计算: 算法沿着染色体"行走",利用HMM的计算方法(如前向-后向算法),结合观测到的杂合/纯合序列、预设的(或需要估计的)突变率、重组率以及状态间的转移概率,计算在基因组的每个位置上,处于各个离散TMRCA状态的可能性。
- TMRCA分布估计: 整合整个基因组的信息,得到一个全局的TMRCA分布,即基因组中不同片段的共同祖先分别落在各个时间区间的比例。
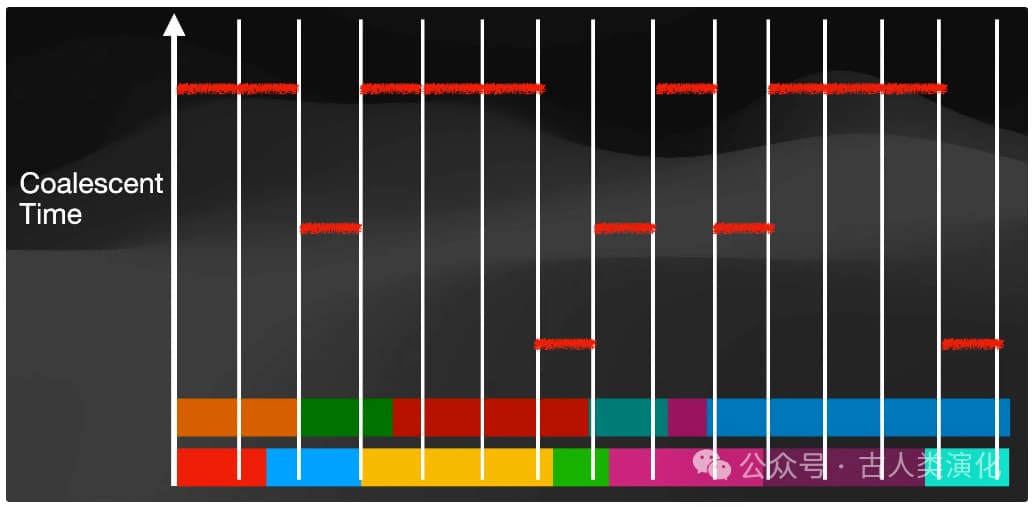
- (N_e)历史推断: (Metaphorically) "rotate" the TMRCA distribution (from step 3). Using the core relationship from coalescent theory mentioned earlier—that the coalescence rate (reflected in the TMRCA distribution) is inversely proportional to effective population size (Ne)—convert the inferred TMRCA distribution into estimates of (N_e) for different past time periods.
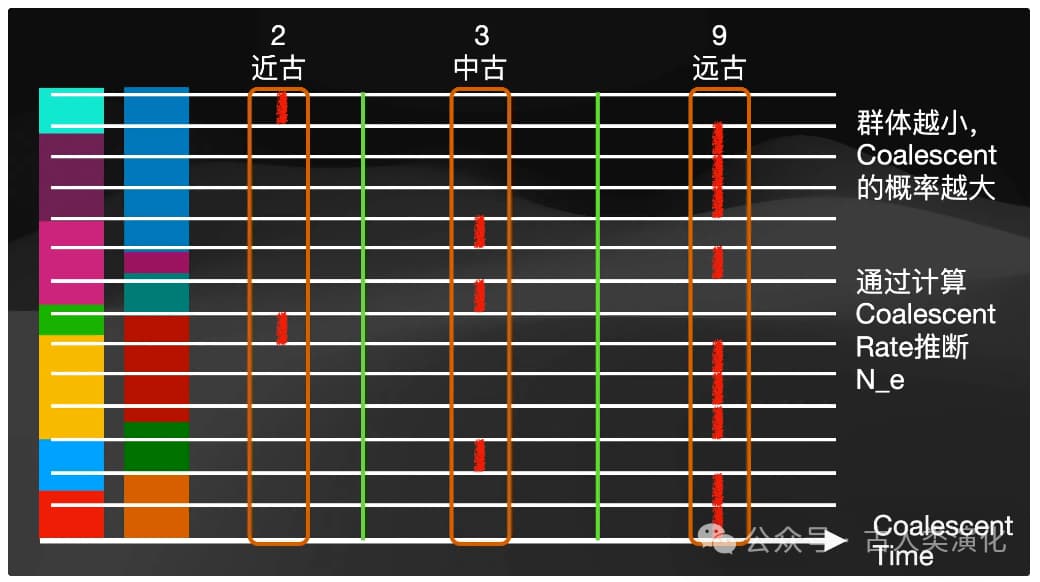

- 输出: 最终结果通常以图表形式展示,横轴是对数时间(过去在左,现在在右),纵轴是对数有效种群大小(N_e)。图中的曲线描绘了种群规模随时间的变化。同时,算法也会给出估计的总体平均(标度化)突变率(\theta_0)和重组率。需要注意的是,输出的时间和种群大小是经过标度化的,需要用户提供真实的每代突变率(\mu)和世代时间(g)才能转换为绝对单位(如年、个体数)。
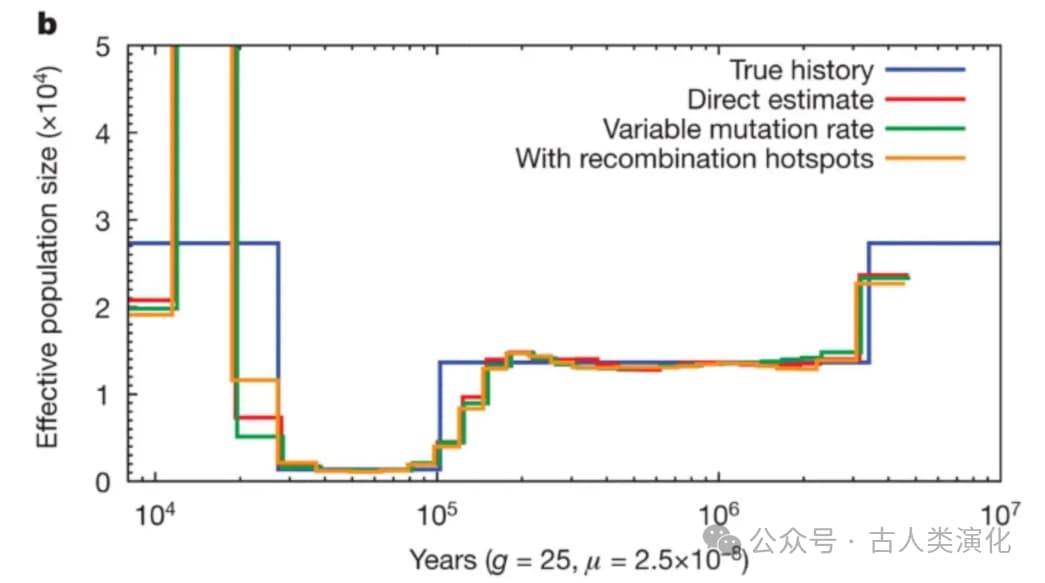
在理解PSMC的工作原理时,我们必须面对一个关键问题,即时间离散化的两难处境。标准HMM框架要求隐藏状态是离散的,但PSMC试图推断的TMRCA本质上是连续的时间值。因此,PSMC不得不将连续的时间轴切割成离散的区间(bins)。这种离散化是一种近似 ,它不可避免地会带来一些问题。首先,它可能导致偏差(bias),因为真实的TMRCA可能恰好落在两个区间的边界附近,或者所选的区间划分方式不能很好地反映真实的TMRCA分布模式,尤其是在时间区间的边界处可能产生人为的波动。其次,HMM算法的计算复杂度通常与状态数量(即时间区间的数量(T))有关,至少是(O(T)),甚至可能是(O(T^2)) 。这意味着增加时间区间的数量以提高分辨率会显著增加计算成本。因此,时间离散化不仅是PSMC模型的一个潜在误差来源,也是其计算效率的一个瓶颈。认识到这一点,对于理解后续算法(如Gamma-SMC、XSMC等试图避免离散化的方法)的发展动机至关重要。
PSMC揭示了什么:穿越时空的种群之旅
PSMC的输出图表为我们提供了一扇观察过去的窗口。图的横轴代表时间(通常以对数尺度表示,越往左越古老),纵轴代表有效种群大小(N_e)(也常用对数尺度)。曲线向上倾斜表示种群扩张,向下倾斜则表示种群收缩或遭遇瓶颈。在其最初的应用中,PSMC为我们描绘了一幅关于人类史前史的壮丽画卷:
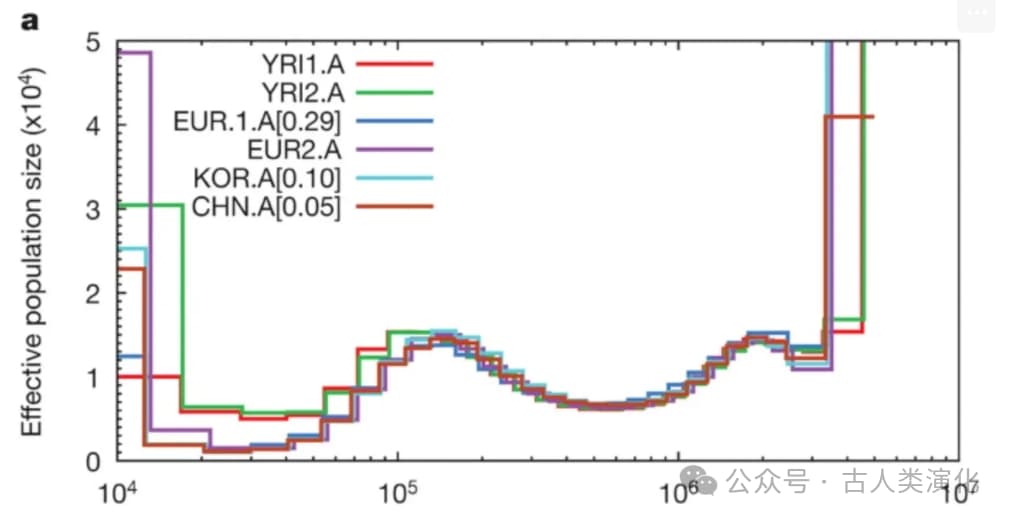
- 所有现代人类群体(非洲、欧洲、亚洲)在距今约15-20万年之前,共享着非常相似的种群历史,拥有相对较大的有效种群规模。
- 非洲人群(如约鲁巴人)也经历了一次瓶颈,但程度较轻,且恢复得更早。
- 在距今约6-25万年间,所有人群的有效种群规模都显得异常高,这可能反映了当时存在着古老的种群亚结构(即人群并非完全随机混合。
- PSMC的结果还暗示,现代人类的遗传分化可能早在10-12万年前就开始了,但不同人群间显著的基因交流可能一直持续到距今2-4万年前才基本停止。(该观点在分化时间和交流事件上众说纷纭,知识在不断迭代)
PSMC的假设与局限
尽管PSMC功能强大,但它的使用和结果解读需要谨慎,因为它建立在一系列假设之上,并存在固有的局限性。
"随机交配"假设
PSMC的核心假设是,所分析的个体来自一个单一的、巨大的、内部个体完全随机交配的群体(即泛交群体, panmictic population)。然而,越来越多的研究表明,许多物种(包括人类)的历史并非如此简单,常常存在种群结构(population structure),如亚群分化、迁移限制、或者古老的种群混合(admixture)。在这种情况下,PSMC推断出的曲线实际上反映的是逆瞬时合并速率(Inverse Instantaneous Coalescence Rate, IICR),而不是纯粹的有效种群大小(N_e)。当存在种群结构时,来自不同亚群的谱系需要更长的时间才能合并,这会人为地拉长TMRCA的分布,使得IICR看起来比真实的(N_e)更大。PSMC会把这种由结构导致的合并延迟误读为过去曾经存在一个更大的种群,或者在合并时间集中的区域误读为种群瓶颈。因此,解读PSMC结果时,必须警惕种群结构可能带来的混淆效应。一个看似剧烈的瓶颈,可能并非真实的种群崩溃,而是反映了古老的亚群分化或基因流减弱。
时间分辨率的限制
PSMC对于推断非常近代的历史(例如,对人类而言,大约是2-3万年以内)能力有限。这是因为在这么短的时间内,一个二倍体基因组的两条链之间发生的重组事件相对较少,不足以产生足够多的TMRCA变化来精确解析近期的种群动态。同样,对于非常远古的历史(例如,对人类而言,超过100-300万年),由于突变可能达到饱和,或者重组信息丢失,PSMC的推断能力也会下降。此外,PSMC倾向于将历史上突然发生的种群规模剧变(如瞬间的瓶颈或扩张)平滑化,难以捕捉其瞬时性。
自然选择的影响
PSMC假设分析的基因组区域是中性的,即不受自然选择的影响。然而,自然选择(如正选择驱动的选择性清除(selective sweeps),或负选择导致的背景选择(background selection, BGS))会改变局部的遗传多样性模式,从而干扰PSMC的推断 。特别是背景选择,它会降低连锁区域的有效种群大小,使得PSMC错误地推断出种群收缩或瓶颈,尤其是在近代。
认识到PSMC的这些局限性,对于理解后续方法的发展至关重要。可以说,PSMC的每一个弱点都成为了催生新算法的动力。例如,为了提高对近代历史的分辨率并利用更多样本信息,MSMC应运而生 。为了处理更大规模的样本并整合等位基因频率信息,SMC++被开发出来 。为了校正自然选择带来的偏差,PSMC+被提出 。为了更准确地模拟种群结构和混合,cobraa、IS-MSMC和MSMC-IM等方法被设计出来 。为了克服时间离散化的问题并提高计算效率,Gamma-SMC、XSMC和diCal等方法采用了不同的策略 。因此,PSMC之后的SMC类方法发展史,清晰地展示了科学研究中"发现问题 → 解决问题"的迭代进步过程。
结语
PSMC及其后续发展的方法,无疑为我们从基因组序列中挖掘种群历史信息提供了前所未有的强大工具,深刻改变了我们对生命演化的认知 。它们让我们能够量化过去的种群波动,将其与气候变化、地理事件、物种形成等宏观过程联系起来。
然而,正如所有科学工具一样,这些基于模型的推断方法并非完美无缺。它们依赖于特定的数学假设(如马尔可夫性、特定的重组和合并模型)和生物学假设(如泛交、中性进化。当这些假设与现实偏离时,结果的解读就需要格外小心。种群结构、自然选择、数据质量等因素都可能对推断产生干扰。因此,在实际应用中,研究者往往需要结合多种分析方法、利用来自不同来源(如考古学、古气候学)的证据,进行综合判断。
令人兴奋的是,这个领域仍然在飞速发展。新的算法不断涌现,它们变得更加复杂、更具扩展性、对各种生物学现实的模拟也更加精细和稳健 。从处理选择和结构的偏差,到整合更多类型的数据,再到提高计算效率和推断精度,研究者们正不懈努力,希望更准确、更全面地解读那部编码在我们细胞核内的、关于生命演化和我们自身来源的DNA双螺旋所蕴含的信息。阅读基因组这部历史书的旅程还远远没有结束。
